To Dr. John Fawcett and Dr. Luana Bulat - Virtual Tree

0x01. Hello!

Hello, Dr. John Fawcett and Dr. Luana Bulat, thank you for viewing this article. This work is about Virtual Tree, an algorithm designed to improve the time complexity of doing dynamic programming on trees.

0x02. An Example of Virtual Tree

Dr. John Fawcett said that we can set up lots of questions based on water flowing through a pipe.

Imagine that: there are $n$$n$ houses and there are also $n-1$$n-1$ water pipes connecting each of them, a group of evil aliens occupied the first house for no reason (they might like the number $1$$1$), now these aliens are planning to attack $k$$k$ houses through water pipe (they are liquid creatures!). We are now given that the details of these $n-1$$n-1$ water pipes (where it starts from, where it ends and the cost of cutting it), we are required to destroy certain pipes so that these aliens cannot attack any of their targets. What is the lowest cost of doing this.

For example, there are ten houses and they are connected like this:

To prevent these aliens reaching any targets, the lowest cost is 5: we only need to cut the 1 -> 2 pipe and 1 -> 3.

It is a very basic dynamic programming on trees question and the state transition equation is not hard to think of.

Let:

1. $i$$i$ represent the current node we are working on, $j$$j$ represent a certain son of $i$$i$

2. $v(i->j)$$v(i->j)$ represent the cost of cutting the pipe which connects $i$$i$ and $j$$j$.

3. $f(i)$$f(i)$ represent the minimum cost of preventing aliens reaching its targets in the subtree of $i$$i$.

   According to the clarification to variables, we have got the state transition equation: $f(i)=\sum min(f(j),v(i->j))$$f(i)=\sum min(\ f(j),v(i->j)\ )$.

0x03. Complicated Situation & Virtual Tree

Clearly, if we do not apply any improvements to that implement, the time complexity is $O(n)$$O(n)$ which is fine when $n$$n$ is small. However, the efficiency of this implement is low as it considers some irrelevant nodes. To improve the efficiency of it, we need to predict which node is needed and which is not, that is the job for virtual tree to handle.

A virtual tree is a simplified edition of original tree for the reason that it only saves necessary nodes.

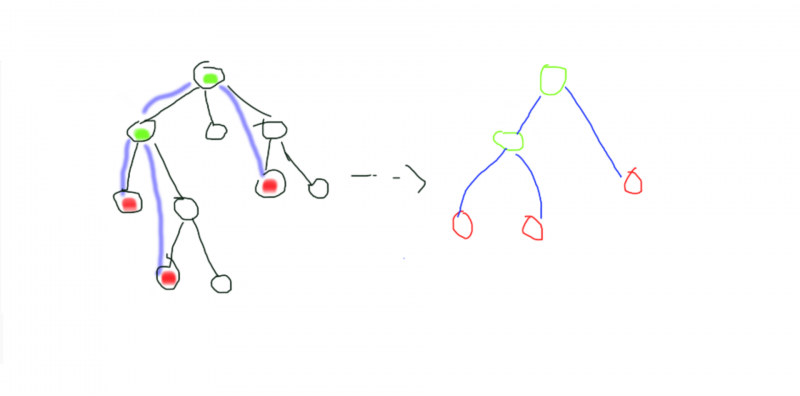
The left hand side tree is the original tree and the right hand side is a virtual tree

0x04. Build And Apply Virtual Tree

In this question, because we only need to consider the targets so we can build a virtual tree includes and only includes the targets and their lowest common ancestors.

The process is below ($LCA(a,b)$$LCA(a,b)$ means the lowest common ancestor of nodes $a$$a$ and $b$$b$):

for i = 1 to Number of Targets:
    A[i] = Target ID
    Flag[Target ID] = IN
Sort array A by ID from smallest to largest
for i = 2 to The Size Of Array A:
    if Flag(LCA(A(i-1),A(i))) is not IN then:
        Add LCA(A(i-1),A(i)) to Array A
if Flag(ROOT) is not IN then:
    Add ROOT to Array A

Now array A is the virtual tree, we can do the dynamic programming on A (because this is graph is a tree, so I prefer using edge list).

Here is the enhanced complete code (written in $C++$$C++$) for Codeforces Round #339 Div. 1 (in this question the value of the each edge is $1$$1$, but in my code, $i_{th}$$i_{th}$ edge has a value $m_i$$m_i$):

xxxxxxxxxx
#include<bits/stdc++.h>
using namespace std;
inline int read(){
    int x=0,f=1;char c=getchar();
    while (!isdigit(c)){if (c=='-')f=-1;c=getchar();}
    while (isdigit(c))x=x*10+c-48,c=getchar();
    return x*f;
}
#define maxn 300005
#define maxp 27
#define LL long long
int lnk[maxn],nxt[2*maxn],son[2*maxn],w[2*maxn],p[4*maxn],top,stk[maxn],d[maxn],in[maxn],out[maxn],dfu,m[maxn],fah[maxn][maxp],q,isi[maxn],n,tot;
LL f[maxn];
void dfs(int x,int fa,int len){
    in[x]=++dfu,m[x]=min(len,m[fa]);
    d[x]=d[fa]+1,fah[x][0]=fa;
    for (int i=lnk[x];i;i=nxt[i])if (son[i]^fa)dfs(son[i],x,w[i]);
    out[x]=++dfu;
}
inline void init(){
    for (int j=1;(1<<j)<=n;j++)
    for (int i=1;i<=n;i++)fah[i][j]=fah[fah[i][j-1]][j-1];
}
inline int lca(int x,int y){
    if (d[x]>d[y])swap(x,y);
    int delta=d[y]-d[x];
    for (int k=0;(1<<k)<=delta;k++)if (delta&(1<<k))y=fah[y][k];
    if (x^y){
        for (int k=log2(n);k>-1;k--)if (fah[x][k]^fah[y][k])x=fah[x][k],y=fah[y][k];
        return fah[x][0];
    }else return y;
}
inline bool cmp(int x,int y){
    int tx=x>0?in[x]:out[-x],ty=y>0?in[y]:out[-y];
    return tx<ty;
}
inline void add(int x,int y,int z){
    w[++tot]=z,son[tot]=y,nxt[tot]=lnk[x],lnk[x]=tot;
}
int main(){
    n=read();
    for (int i=1;i<n;i++){
        int x=read(),y=read(),z=read();
        add(x,y,z),add(y,x,z);
    }
    m[1]=m[0]=0x7fffffff,dfs(1,0,0x7fffffff),init();
    q=read();
    for (int t=1;t<=q;t++){
        int k=read();tot=0;
        for (int i=1;i<=k;i++){
            int x=read();
            isi[p[++tot]=x]=1,f[x]=m[x];
        }
        sort(p+1,p+1+tot,cmp);
        for (int i=2;i<=tot;i++){
            int ff=lca(p[i-1],p[i]);
            if (!isi[ff])isi[p[++tot]=ff]=1;
        }
        int tt=tot;
        for (int i=1;i<=tt;i++)p[++tot]=-p[i];
        if (!isi[1])p[++tot]=1,p[++tot]=-1;
        sort(p+1,p+1+tot,cmp);
        for (int i=1;i<=tot;i++){
            if (p[i]>0){stk[++top]=p[i];continue;}
            int now=stk[top],ff=stk[--top];
            if (now^1)f[ff]+=min((long long)(m[now]),f[now]);
                   else{printf("%lld\n",f[1]),isi[1]=0,f[1]=0;break;}
            isi[now]=0,f[now]=0;
        }
    }
    return 0;
}