浅谈虚树

0x00 预备知识

首先学虚树之前你必须会以下知识：

LCA（什么算法都可以，除了暴力→_→）
欧拉序（这个比较简单，我等下会讲）
栈（这个你都不会那你可以去面壁了）

好了，现在让我们假设你已经会了这些算法，那么你就可以去看看这道题目了，本道题目将是本文的例题。

题目链接：https://www.lydsy.com/JudgeOnline/problem.php?id=2286

你应该一眼就看出来这题应该用 $树形DP$ 了吧？没有？那也没关系。让我们定义 $f[i]$ 表示切断 $i$ 的所有子树中的资源丰富的节点的最优代价。转移方程显然就是： $f[i]+=min(f[j],v[j])$ ， $v[i]$ 表示切断 $j->ij$ 这一条路的代价，解释为：要不就将 $j$ 的子树中的所有资源丰富的点切掉，要不就干脆把 $j->i$ 这一整条路切掉。但是呢，我们又发现，这个 $k$ 实在是太大了，显然普通的 $树形DP$ 是无法满足要求的，这时候就需要虚树来优化时间复杂度。

0x01 什么是虚树？

什么是虚树？想必很多人看到了这个名字肯定就觉得这是一棵“不存在的树“，实际上恰恰相反，虚树不仅是存在的，而且还是主树（就是原树）的一个代表。什么意思？就是说，虚树去除了主树了一些不必要的节点，但是又比较完整地保留了主树的特征。举个例子（下图源于洛谷 | 计算机科学教育新生态，侵删）：

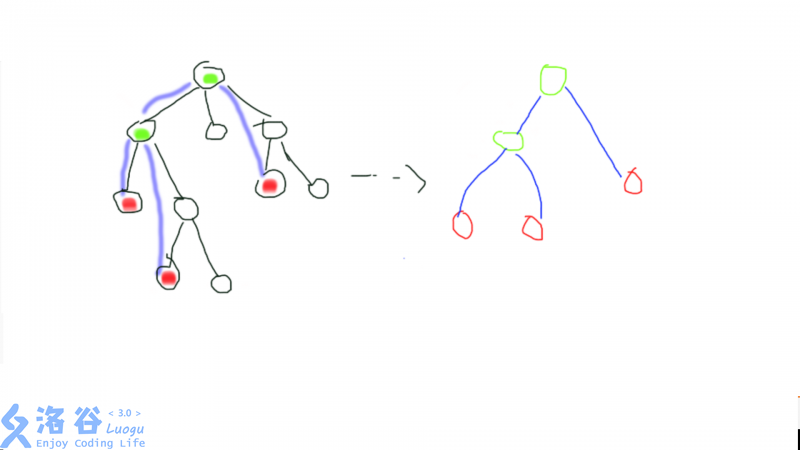
左图是主树，右图是”精简改良“后的虚树，发现了什么没有？其实虚树就是删除了主树的一些节点，在不改变原来相对顺序的情况下建立的一棵树，至于要选什么点来加入到虚树，我之后会讲。因为虚树精简了原树，所以在虚树上遍历的时间效率会提高很多！

0x02 欧拉序

何为欧拉序？在我的理解就跟 $DFS$ 序差不多，就是入度记一次、出度记一次。举个栗子：（下图来源于dfs序和欧拉序 - Styx-ferryman - 博客园，侵删）：

那么这棵树的欧拉序就是：A-B-D-B-E-G-E-B-A-C-F-H-F-C-A 。

问：欧拉序有什么用啊？

答：别看欧拉序比较简单，欧拉序的用处可是很多的。比如说求 $LCA$ 。

问：如何用欧拉序求LCA？

答：只需要求得两点欧拉序之间深度最小的点就可以了（为什么？请读者自己思考）。另外，你把话题带偏了，我们要介绍的是虚树！

0x03 虚树的建立

~~众所周知虚树建立是很简单的~~（拖下去打）

但是其实虚树的建立真的很简单，在大多数情况下，虚树其实就是存入节点和出节点，那么存点的标准是什么呢？以本题为例，我们发现实际上影响答案的应该就只有资源丰富的节点和这些节点们的 $LCA$ 以及根节点，那我们只需要往数组里存这些节点就好了。

实现代码如下：


xxxxxxxxxx
    int k=read();tot=0;
    for (int i=1;i<=k;i++){
        int x=read();
        isi[p[++tot]=x]=1,f[x]=m[x]; //存入资源丰富的点，并且初始化f[]数组
    }
    sort(p+1,p+1+tot,cmp);
    for (int i=2;i<=tot;i++){
        int ff=lca(p[i-1],p[i]);  //求得资源丰富的点之间的LCA
        if (!isi[ff])isi[p[++tot]=ff]=1;  //如果没有被记录过，那么加入虚树
    }
    int tt=tot;
    for (int i=1;i<=tt;i++)p[++tot]=-p[i]; //正的为进节点，负的为出节点（正负仅为判断）
    if (!isi[1])p[++tot]=1,p[++tot]=-1; //如果根节点（1）没有加入到虚树中，那么就加入

0x04 虚树的应用

现在我们已经建立了虚树，那么怎么应用呢？肯定是遍历这棵虚树啊！那么怎么遍历呢？因为考虑到虚树建立的特殊性，我们很难通过普通的领接表去 $DFS$ 遍历整棵树，但是我们突然又想到：为何要用 $DFS$ ？ $DFS$ 不就是相当于开了一个隐性的栈吗（这个如果不理解的话，请跟着 $DFS$ 模拟一遍，然后你就会明白了 ~(≧▽≦)/~啦啦啦），那么我们不能直接使用 $DFS$ 为何我们不直接开个栈去模拟 $DFS$ 呢？所以至此，虚树就讲完了，需要注意的是，由于本题是 $树形DP$ ，所以需要根据欧拉序排序，保证是儿子推到父亲（否则那还不玩完？）。

代码如下：


xxxxxxxxxx
        sort(p+1,p+1+tot,cmp); //根据欧拉序排序
        for (int i=1;i<=tot;i++){
            if (p[i]>0){stk[++top]=p[i];continue;} //如果是进入点，那么就将该点存到栈中
            int now=stk[top],ff=stk[--top]; //由于已经排过序，所以栈的下一个一定是该节点的父亲（读者可以将这两个变量输出来然后感性理解一下^_^）
            if (now^1)f[ff]+=min((long long)(m[now]),f[now]); //DP
                   else{printf("%lld\n",f[1]),isi[1]=0,f[1]=0;break;} //如果已经遍历到根节点那么就输出答案
            isi[now]=0,f[now]=0; //由于遍历该节点一次后就不会遍历第二次，那么不妨将这个节点的一些信息清空，免得下次还要memset浪费时间
        }

0x05 虚树流程总结

虚树的流程不外乎于一下几个步骤：

拣选合适的点建立虚树 $->$ 开栈模拟 $DFS$ 遍历整棵虚树，完成自己的程序。

所以说虚树其实就是用栈来优化毫不为过。

0x06 我的完整代码

以例题为例：


xxxxxxxxxx
#include<bits/stdc++.h>
using namespace std;
inline int read(){
    int x=0,f=1;char c=getchar();
    while (!isdigit(c)){if (c=='-')f=-1;c=getchar();}
    while (isdigit(c))x=x*10+c-48,c=getchar();
    return x*f;
}
#define maxn 300005
#define maxp 27
#define LL long long
int lnk[maxn],nxt[2*maxn],son[2*maxn],w[2*maxn],p[4*maxn],top,stk[maxn],d[maxn],in[maxn],out[maxn],dfu,m[maxn],fah[maxn][maxp],q,isi[maxn],n,tot;
LL f[maxn];
void dfs(int x,int fa,int len){
    in[x]=++dfu,m[x]=min(len,m[fa]);
    d[x]=d[fa]+1,fah[x][0]=fa;
    for (int i=lnk[x];i;i=nxt[i])if (son[i]^fa)dfs(son[i],x,w[i]);
    out[x]=++dfu;
}
inline void init(){
    for (int j=1;(1<<j)<=n;j++)
    for (int i=1;i<=n;i++)fah[i][j]=fah[fah[i][j-1]][j-1];
}
inline int lca(int x,int y){
    if (d[x]>d[y])swap(x,y);
    int delta=d[y]-d[x];
    for (int k=0;(1<<k)<=delta;k++)if (delta&(1<<k))y=fah[y][k];
    if (x^y){
        for (int k=log2(n);k>-1;k--)if (fah[x][k]^fah[y][k])x=fah[x][k],y=fah[y][k];
        return fah[x][0];
    }else return y;
}
inline bool cmp(int x,int y){
    int tx=x>0?in[x]:out[-x],ty=y>0?in[y]:out[-y];
    return tx<ty;
}
inline void add(int x,int y,int z){
    w[++tot]=z,son[tot]=y,nxt[tot]=lnk[x],lnk[x]=tot;
}
int main(){
    n=read();
    for (int i=1;i<n;i++){
        int x=read(),y=read(),z=read();
        add(x,y,z),add(y,x,z);
    }
    m[1]=m[0]=0x7fffffff,dfs(1,0,0x7fffffff),init();
    q=read();
    for (int t=1;t<=q;t++){
        int k=read();tot=0;
        for (int i=1;i<=k;i++){
            int x=read();
            isi[p[++tot]=x]=1,f[x]=m[x];
        }
        sort(p+1,p+1+tot,cmp);
        for (int i=2;i<=tot;i++){
            int ff=lca(p[i-1],p[i]);
            if (!isi[ff])isi[p[++tot]=ff]=1;
        }
        int tt=tot;
        for (int i=1;i<=tt;i++)p[++tot]=-p[i];
        if (!isi[1])p[++tot]=1,p[++tot]=-1;
        sort(p+1,p+1+tot,cmp);
        for (int i=1;i<=tot;i++){
            if (p[i]>0){stk[++top]=p[i];continue;}
            int now=stk[top],ff=stk[--top];
            if (now^1)f[ff]+=min((long long)(m[now]),f[now]);
                   else{printf("%lld\n",f[1]),isi[1]=0,f[1]=0;break;}
            isi[now]=0,f[now]=0;
        }
    }
    return 0;
}

0x07 推荐练习题

1.BZOJ4912 天才黑客

2.BZOJ3572 世界树