替罪羊树算法总结

0.替罪羊树算法简述

平衡树是一种一种优化算法，其功能是防止二叉搜索树在进行插入操作时变成一条树链从而使得查询效率低下。平衡树的实现有很多种方式，其中替罪羊树是一种十分特立独行的种，别的平衡树进行平衡操作时大多数都是要用旋转的，即使某些平衡树树不用旋转操作（朝鲜树）但其复杂度令人堪忧。替罪羊树的核心操作只是暴力重建不平衡的子树，从而达到使树平衡的效果，而且替罪羊树的效率十分高，如果除去reverse等不寻常操作，而是单单只有insert、erase等操作的话，替罪羊树的效率稳居第一名的宝座，具体请见某度贴吧中的这条帖子

1.替罪羊树的一些常规变量

这里简单介绍一下替罪羊树的一些简单变量

 
struct ypc{
    int val,fa,son[2]; //val表示该点的权值，fa表示该点的父亲节点编号，son[0..1]表示该点的左右儿子编号
    double size; //size表示包括以该点为根节点的数的大小
}t[400010];

2.平衡因子α

在讲替罪羊树的各种操作之前，读者们要先了解一下替罪羊树的一个十分重要的常数——平衡因子$α$。刚才讲过了，替罪羊树是靠重建树来实现使树平衡的，但是什么时候才重建树？这时候我们就需要一个判断标准来判断这个节点是否失衡，这个判断一句就是 父亲节点的$size*α>=$$左儿子的size、右儿子的size。$ 代码如下：

 
xxxxxxxxxx
inline bool balance(int id){
    return t[t[id].son[0]].size<=t[id].size*alpha&&t[t[id].son[1]].size<=t[id].size*alpha;
}

由此可见，替罪羊树的的疏密程度与平衡因子α有很大的关系，查询效率也因阿尔法大小而异，大多数情况下α的赋值范围在$0.5$~$1$之间（在普通情况下，$α$赋值为$0.75$就可以了），当然特殊情况特殊处理α的大小还需因实际情况而定（不排除用动态$α$来适应各种不同的数据情况，当然很少见），这里给出一张从知乎偷来的α的取值对于程序性能的影响的图表…… 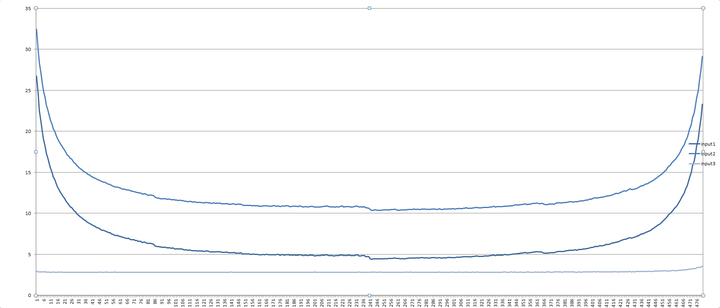我们可以发现，$α$取值越靠近两端时间效率越大，当$α$取值在$0.5$~$0.8$左右浮动的时候，程序的效率还是挺不错的。

3.重建树

这个操作是替罪羊树的重头戏，是替罪羊树的核心操作，重建树的过程有3个过程，分别是：获取当前这棵失衡的树的所有节点编号，中序遍历建树，重新建树（这里的重新建树相当于是调取了上面两个函数之后再做一些扫尾的工作）。 首先第一个操作十分简单，只需要用dfs递归一下就行了，代码如下：

 
xxxxxxxxxx
inline void dfs(int id){
    if (!id)return;
    dfs(t[id].son[0]);
    cur[++sum]=id;
    dfs(t[id].son[1]);
}

第二个操作也没有什么难度，首先先得到当前[L,R]区间的中间的编号，然后在去以$[L,mid-1]$为区间建树，$[mid+1,R]$为区间建树就OK了，最后不要忘记改一下节点的左右儿子，节点的$size$，左右儿子的父亲节点编号（即当前这个节点编号），代码如下：

 
xxxxxxxxxx
inline int build(int L,int R){
    if (L>R)return 0;
    int mid=qmid(L,R)/*取中函数*/,id=cur[mid],ls=build(L,mid-1),rs=build(mid+1,R);
    t[id].son[0]=ls,t[id].son[1]=rs,
    t[ls].fa=id,t[rs].fa=id,
    t[id].size=t[ls].size+t[rs].size+1;
    return id; //返回这个当前节点编号
}

第三个操作依然没有什么难度，无非就是调用上面两个过程之后，再对新子树的根节点进行操作，代码如下：

 
xxxxxxxxxx
inline int get_lr(int id){ //判断着当前节点是它的父亲的左儿子还是右儿子
    return t[t[id].fa].son[1]==id;
}
inline void rebuild(int id){
    sum=0/*计数用的变量赋初值*/,dfs(id);
    int fa=t[id].fa,opt=get_lr(id),new_son=build(1,sum);//fa记录原节点的父亲，new_son是fa的新儿子
    t[new_son].fa=fa,t[fa].son[opt]=new_son;
    if (root==id)root=new_son; //如果重建的是整棵树，那么根节点就应该是新儿子（new_son）了
}

4.插入操作

插入操作和二叉搜索树没有什么大区别，也是比当前节点小的就插到左子树否则就插到右子树，有两点需要注意：插入元素的时候记得一路更新size、插入完成后要判断子树有无失衡，如果失衡就重建树。 代码如下：

 
xxxxxxxxxx
inline void insert(int x){
    int tmp=root;
    while (1){
        t[tmp].size++; //更新size
        int fa=tmp,opt=(x>=t[tmp].val);tmp=t[tmp].son[opt];
        if (!tmp){ //如果没有tmp为0就插入
            t[++tot].size=1,t[tot].val=x,t[tot].fa=fa,t[fa].son[opt]=tot;
            break;
        }
    }
    int flg=0;
    for (int i=tot;i;i=t[i].fa)if (!balance(i))flg=i; //如果失衡了，就记录该节点的编号，方便重建
    if (flg)rebuild(flg);
}

5.删除操作

删除操作也是替罪羊树的一个特色操作，其主要的核心就是帮助这个节点找替罪羊。 打个比方：比如说你要删x节点，如果这个节点没有左子树或者右子树，那么就直接删掉完事儿（这个节点是树链中的一个节点，删了它然后重新接上这条链依然不影响这棵树的平衡性），否则的话我们需要找这个节点的左子树的最后一个节点，因为这个节点满足一个性质，比该节点小（也就是比右子树的所有节点权值都要笑），但是又比其它的左子树的节点的权值都大，把这个节点当成替罪羊节点不会破坏树的性质，当然还有些人会将这个节点的右子树的第一个节点来当做替罪羊节点，其实道理都一样。那么之后的删除操作就拿这个替罪羊节点开刀，然后把这个替罪羊的节点的权值赋值给这个要被删除的节点，让这个替罪羊节点以另外一种形态“生活”下去，举个例子（每个节点上的数字即为这个节点的编号）：

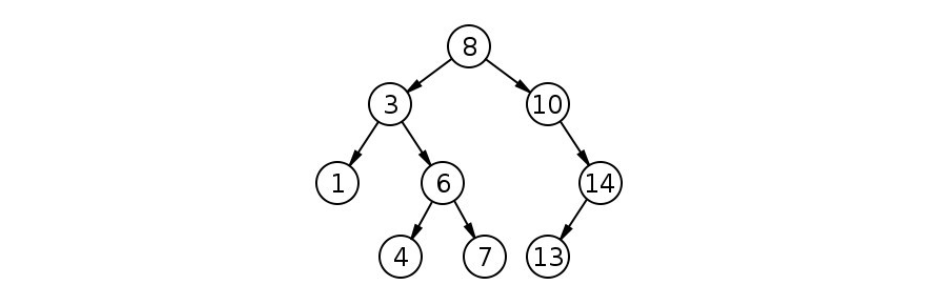
这里有一颗替罪羊树，现在我们要把$3$号节点删除，那么怎么删呢？

首先我们发现$3$号节点有左子树，那么就往下查找，发现了$1$号节点，然后就开始删除操作：首先先将$1$号节点的信息给予$3$号节点，然后删了$1$号节点，那么这棵树就变成了这样

$1$号节点被删除了，但是$3$号节点代替了$1$号节点继续存活了下来（有没有一点悲壮的意味？）

代码如下：

 
xxxxxxxxxx
inline void erase(int id){
    if (t[id].son[0]&&t[id].son[1]){ //搜寻替罪羊节点
        int tmp=t[id].son[0];
        while (t[tmp].son[1])tmp=t[tmp].son[1];
        t[id].val=t[tmp].val,id=tmp; //找到了节点，替换信息，转而删除替罪羊节点
    }
    int son=t[id].son[0]?t[id].son[0]:t[id].son[1],fa=t[id].fa,opt=get_lr(id);
    t[fa].son[opt]=son,t[son].fa=fa;
    for (int i=fa;i;i=t[i].fa)t[i].size--;
    if (root==id)root=son;
}

一些例题：

1.1：

Luogu3369

这道题就是替罪羊树的模板题（好像是所有平衡树的模板题吧……）。

这道题目包括了替罪羊树的最基本的一些操作，删除，插入，求前驱，求后继之类的操作都是替罪羊树（平衡树）的基本操作。

代码如下：

 
xxxxxxxxxx
#include<cstdio>
#include<algorithm>
#define alpha 0.75
#define qmid(L,R) L+((R-L)>>1)
#define INF 0x7fffffff
using namespace std;
struct ypc{
    int val,fa,son[2];
    double size;
}t[800010];
int n,q,tot,cur[800010],sum,root;
inline int read(){
    int ret=0,flg=1;char ch=getchar();
    while (ch<'0'||ch>'9'){if (ch=='-')flg=-1;ch=getchar();}
    while (ch>='0'&&ch<='9')ret=ret*10+ch-48,ch=getchar();
    return ret*flg;
}
inline bool balance(int id){
    return t[t[id].son[0]].size<=t[id].size*alpha&&t[t[id].son[1]].size<=t[id].size*alpha;
}
inline void dfs(int id){
    if (!id)return;
    dfs(t[id].son[0]);
    cur[++sum]=id;
    dfs(t[id].son[1]);
}
inline int build(int L,int R){
    if (L>R)return 0;
    int mid=qmid(L,R),id=cur[mid],ls=build(L,mid-1),rs=build(mid+1,R);
    t[id].son[0]=ls,t[id].son[1]=rs,t[ls].fa=id,t[rs].fa=id,t[id].size=t[ls].size+t[rs].size+1;
    return id;
}
inline int get_lr(int id){
    return t[t[id].fa].son[1]==id;
}
inline void rebuild(int id){
    sum=0,dfs(id);
    int fa=t[id].fa,opt=get_lr(id),new_son=build(1,sum);
    t[new_son].fa=fa,t[fa].son[opt]=new_son;
    if (root==id)root=new_son;
}
inline void erase(int id){
    if (t[id].son[0]&&t[id].son[1]){
        int tmp=t[id].son[0];
        while (t[tmp].son[1])tmp=t[tmp].son[1];
        t[id].val=t[tmp].val,id=tmp;
    }
    int son=t[id].son[0]?t[id].son[0]:t[id].son[1],fa=t[id].fa,opt=get_lr(id);
    t[fa].son[opt]=son,t[son].fa=fa;
    for (int i=fa;i;i=t[i].fa)t[i].size--;
    if (root==id)root=son;
}
inline int get_front(int x){
    int ret=-INF,tmp=root;
    while (tmp)if (t[tmp].val<x)ret=max(ret,t[tmp].val),tmp=t[tmp].son[1];else tmp=t[tmp].son[0];
    return ret;
}
inline int get_back(int x){
    int ret=INF,tmp=root;
    while (tmp)if (t[tmp].val>x)ret=min(ret,t[tmp].val),tmp=t[tmp].son[0];else tmp=t[tmp].son[1];
    return ret;
}
inline int get_rank(int x){
    int tmp=root,ret=0;
    while (tmp)if (x<=t[tmp].val)tmp=t[tmp].son[0];else ret=ret+t[t[tmp].son[0]].size+1,tmp=t[tmp].son[1];
    return ret;
}
inline void insert(int x){
    if (!root){t[root=++tot].val=x,t[root].size=1,t[root].fa=0;return;}
    int tmp=root;
    while (1){
        t[tmp].size++;
        int fa=tmp,opt=(x>=t[tmp].val);tmp=t[tmp].son[opt];
        if (!tmp){
            t[++tot].size=1,t[tot].val=x,t[tot].fa=fa,t[fa].son[opt]=tot;
            break;
        }
    }
    int flg=0;
    for (int i=tot;i;i=t[i].fa)if (!balance(i))flg=i;
    if (flg)rebuild(flg);
}
inline int get_xth(int x){
    int tmp=root;
    while (1){
        if (t[t[tmp].son[0]].size+1==x)return t[tmp].val;
        if (x<=t[t[tmp].son[0]].size)tmp=t[tmp].son[0];else x-=t[t[tmp].son[0]].size+1,tmp=t[tmp].son[1];
    }
}
inline int get_id(int x){
    int tmp=root;
    while (tmp)if (t[tmp].val==x)return tmp;else tmp=t[tmp].son[x>=t[tmp].val];
    return tmp;
}
int main(){
    q=read();
    for (int i=1;i<=q;i++){
        int tpe=read(),x=read();
        if (tpe==1)insert(x);
        if (tpe==2)erase(get_id(x));
        if (tpe==3)printf("%d\n",get_rank(x)+1);
        if (tpe==4)printf("%d\n",get_xth(x));
        if (tpe==5)printf("%d\n",get_front(x));
        if (tpe==6)printf("%d\n",get_back(x));
    }
    return 0;
}

1.2

Luogu1486

也是模板题，当减工资的时候暴力递归删除员工节点，要注意的就是初始工资小于最低工资的不要添加就行了，剩下的操作就是平衡树的基本操作了。

代码如下：

 
xxxxxxxxxx
#include<cstdio>
#define alpha 0.75
#define qmid(L,R) L+((R-L)>>1)
#define INF 0x7fffffff
using namespace std;
inline int read(){
    int ret=0,flg=1;char ch=getchar();
    while (ch<'0'||ch>'9'){if (ch=='-')flg=-1;ch=getchar();}
    while (ch>='0'&&ch<='9')ret=ret*10+ch-48,ch=getchar();
    return ret*flg;
}
struct ypc{
    int val,fa,son[2];
    double size;
}t[100010];
int n,sum,cur[100010],tot,root,min,money,tot_leave;
inline bool balance(int id){
    return t[t[id].son[0]].size<=t[id].size*alpha&&t[t[id].son[1]].size<=t[id].size*alpha;
}
inline void dfs(int id){
    if (!id)return;
    dfs(t[id].son[0]);
    cur[++sum]=id;
    dfs(t[id].son[1]);
}
inline int build(int L,int R){
    if (L>R)return 0;
    int mid=qmid(L,R),id=cur[mid],ls=build(L,mid-1),rs=build(mid+1,R);
    t[id].son[0]=ls,t[id].son[1]=rs;
    t[ls].fa=id,t[rs].fa=id;
    t[id].size=t[ls].size+t[rs].size+1;
    return id;
}
inline bool get_lr(int id){
    return t[t[id].fa].son[1]==id;
}
inline void rebuild(int id){
    sum=0,dfs(id);
    int fa=t[id].fa,opt=get_lr(id),new_son=build(1,sum);
    t[fa].son[opt]=new_son,t[new_son].fa=fa;
    if (root==id)root=new_son;
}
inline void insert(int x){
    if (!root){if (!tot)tot=1;root=tot,t[root].val=x,t[root].size=1,t[root].fa=0;return;}
    int tmp=root;
    while (tmp){
        t[tmp].size++;
        int fa=tmp,opt=(x>=t[tmp].val);tmp=t[tmp].son[opt];
        if (!tmp){
            t[fa].son[opt]=++tot,t[tot].fa=fa,t[tot].val=x,t[tot].size=1;
            break;
        }
    }
    int flg=0;
    for (int i=tot;i;i=t[i].fa)if (!balance(i))flg=i;
    if (flg)rebuild(flg);
}
inline void erase(int id){
    if (t[id].son[1]&&t[id].son[0]){
        int tmp=t[id].son[0];
        while (t[tmp].son[1])tmp=t[tmp].son[1];
        t[id].val=t[tmp].val,id=tmp;
    }
    int fa=t[id].fa,son=t[id].son[0]?t[id].son[0]:t[id].son[1],opt=get_lr(id);
    t[son].fa=fa,t[fa].son[opt]=son;
    for (int i=fa;i;i=t[i].fa)t[i].size--;
    if (root==id)root=son;
}
inline int erase_val(int x){
//  printf("---------\n");
    int tmp=root;
    while (tmp){
//      printf("%d %d\n",tmp,t[tmp].val+money);
        if (x>t[tmp].val+money){
            sum=0,dfs(t[tmp].son[0]),cur[++sum]=tmp;
            tot_leave+=sum;
            for (int i=1;i<=sum;i++)erase(cur[i]);
            tmp=t[tmp].son[1];
        }else tmp=t[tmp].son[0];
    }
//  printf("---------\n");
}
inline int get_xth(int x){
    int tmp=root;
    while (tmp){
        if (t[t[tmp].son[0]].size==x-1)return t[tmp].val+money;
        if (t[t[tmp].son[0]].size>=x)tmp=t[tmp].son[0];else x-=t[t[tmp].son[0]].size+1,tmp=t[tmp].son[1];
    }
}
int main(){
    n=read(),min=read();
    root=0;
    for (int i=1;i<=n;i++){
        char tpe[2];
        scanf("%s",tpe);
        int x=read();
        if (tpe[0]=='I'&&x>=min)insert(x-money);
        if (tpe[0]=='A')money+=x;
        if (tpe[0]=='S')money-=x,erase_val(min)/*,printf("tot_leave=%d\n",tot_leave)*/;
        if (tpe[0]=='F')printf("%d\n",t[root].size>=x?get_xth(t[root].size-x+1):-1);
    }
    printf("%d\n",tot_leave);
    return 0;
}

1.3

BZOJ3600